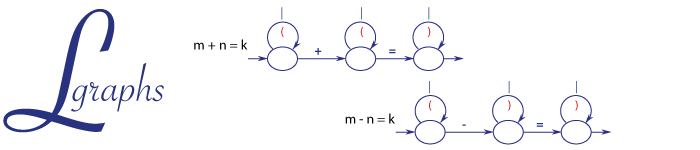Способы описания формальных языков
- формальные грамматики (в частности БНФ)
- автоматы
- выражения
- уравнения
- графы
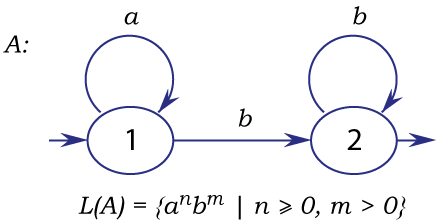
Пример описания регулярного языка с помощью регулярного L-графа
Граф состоит из вершин и дуг, помеченных символами входного алфавита.
Разрешаются непомеченные дуги.
Некоторые вершины выделены как начальные (в них входит стрелка из «ниоткуда» ) и как
заключительные (стрелка выходит в «никуда»).
Успешный путь — это путь на графе из начальной вершины в заключительную.
Пометка пути — это последовательность пометок дуг, составляющих путь.
Язык, который описывает граф, это множество пометок всех успешных путей.
Такой граф по сути представляет собой конечный автомат.
Будем называть такие графы регулярными.
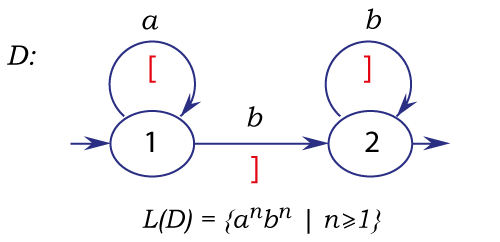
Пример описания бесконтекстного языка с помощью бесконтекстного L-графа
Этот вид графов, назовем их бесконтекстными, отличается от регулярных тем,
что добавлен еще один вид пометок на дугах - скобки.
Скобки могут быть с индексами, т.е. разрешается несколько видов парных скобок.
Успешным путем, или маршрутом, в них считается такой путь, что последовательность его
скобочных пометок представляет собой сбалансированную скобочную систему.
Например, [1 [1 [2 ]2 [1 ]1 ]1 [3 ]3 ]1 является правильной скобочной системой, а
последовательности [ ] [, [ [ ], [1 [2 ]1 ]2 таковыми не являются. Разрешаются «нейтральные» дуги, не помеченные скобками.
Поэтому регулярный граф является частным случаем графа бесконтекстного.
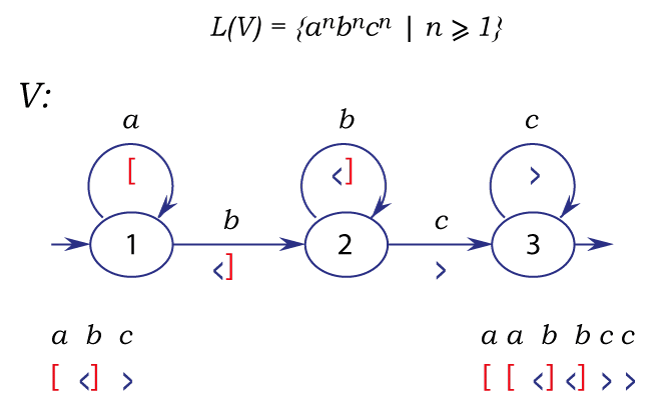
Пример описания контекстно-зависимого языка с помощью L-графа
Это пример L-графа (от слова Language). По сравнению с бесконтекстными добавлен еще один вид пометок — скобки другого цвета (синие) ( их также можно отличать по форме — угловые).
Итак, теперь есть две независимые скобочные пометки — красные (квадратные ) и синие (угловые). Синие скобки также могут иметь индексы.
Успешный путь в L-графе должен быть сбалансирован как по красным (квадратным), так и по синим (угловым) скобкам. Например, [ ⟨ ] ⟩ — сбалансированная система по обеим формам скобок.
По своей описательной силе L-графы сравнимы с машиной Тьюринга, так что с помощью них можно описывать не только контекстно-зависимые языки, но и языки более широких классов (рекурсивные, рекурсивно - перечислимые).
Иерархия графов
Бесконтекстный граф является частным случаем L –графа. Таким образом получаем иерархию графовых описаний языков:
- Регулярные графы
- Бесконтекстные графы
- L-графы
Арифметика на L-графах
С помощью L-графов можно описать языки, представляющие в унарной (палочковой) системе счисления такие операции как сложение, вычитание, умножение, возведение в степень и др.
Сложение
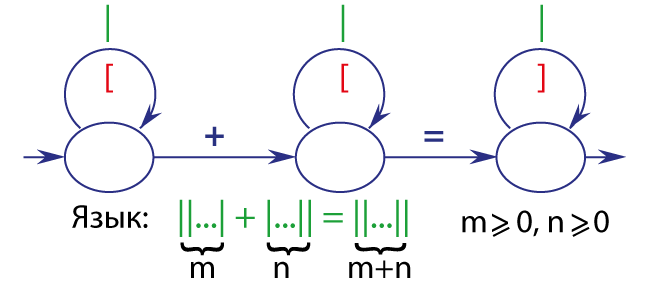
Вычитание
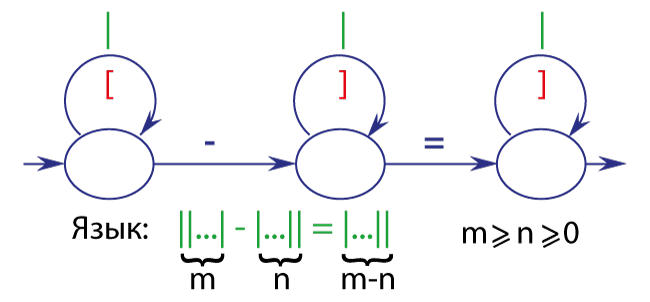
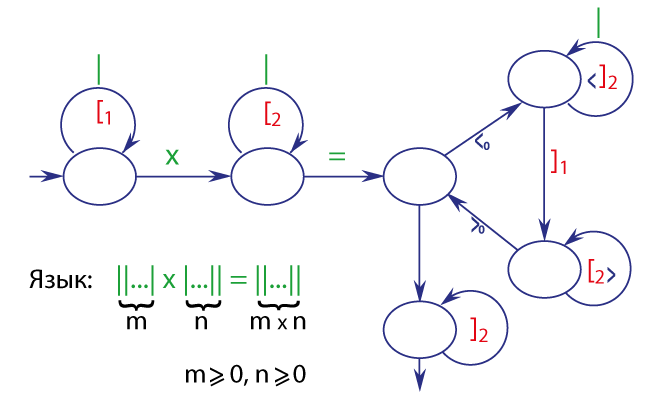
Умножение на шести вершинах
Идея Артема Ростовского, 2011 год
Показательная функция
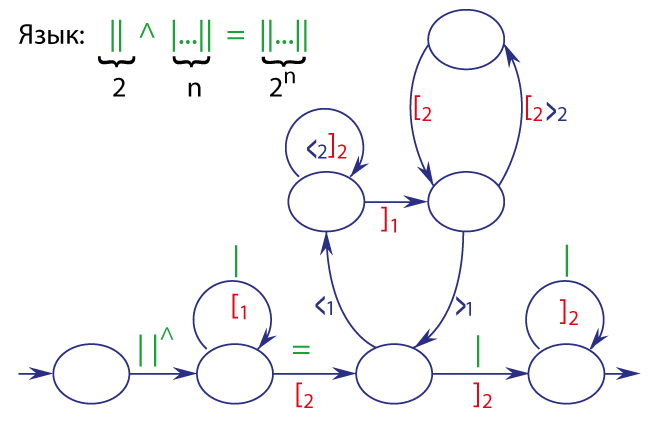
Степенная функция
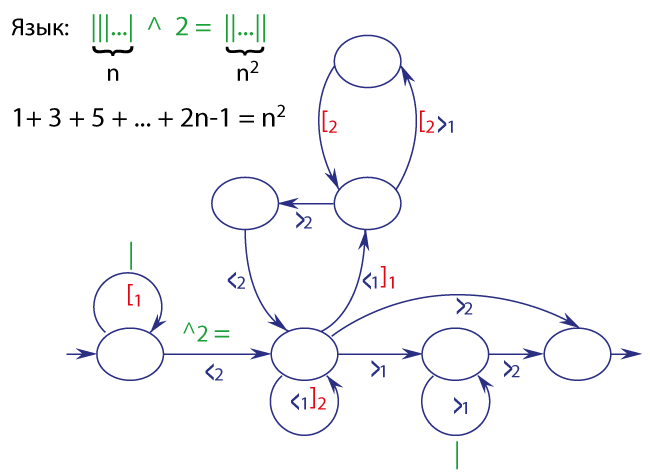
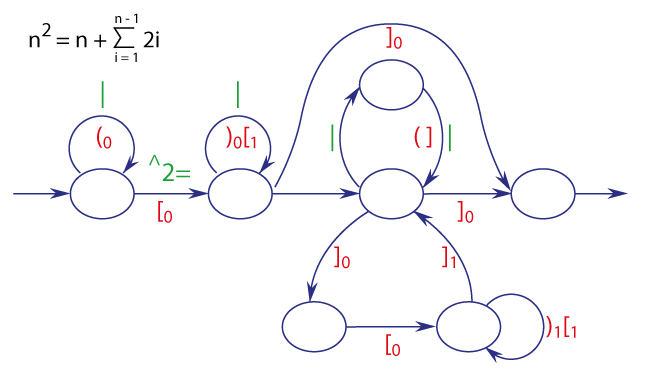
Квадратичная функция
Идея Никиты Лобосова, 2016 год
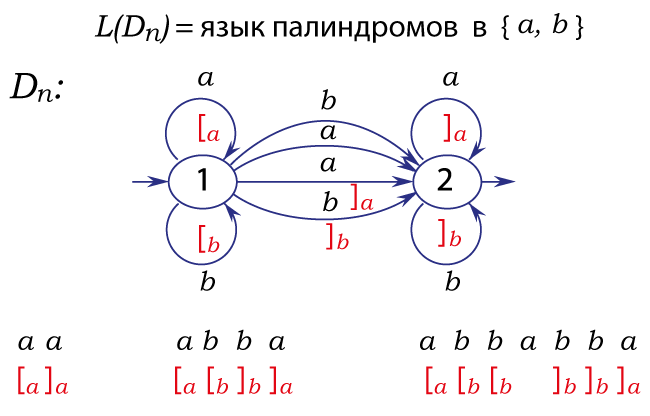
Язык палиндромов
Участниками семинара являлись ранее Л.И.Станевичене, В.В.Игнатов, П.Г.Сутырин. Их работа послужила предтечей нынешних разработок в области L-графов.